I conceive that the chief aim of the physicist in discussing a theoretical problem is to obtain ‘insight’—to see which of the numerous factors are particularly concerned in any effect and how they work together to give it. For this purpose a legitimate approximation is not just an unavoidable evil; it is a discernment that certain factors—certain complications of the problem—do not contribute appreciably to the result. We satisfy ourselves that they may be left aside; and the mechanism stands out more clearly freed from these irrelevancies. This discernment is only a continuation of a task begun by the physicist before the mathematical premises of the problem could even be stated; for in any natural problem the actual conditions are of extreme complexity and the first step is to select those which have an essential influence on the result—in short, to get hold of the right end of the stick. —A. S. Eddington
Browse any internet martial arts forum long enough and one is almost certain to find a heated physics debate. Although the questions raised run the gamut from whether or not the heel should be raised during a reverse punch to the definition of kime, there seems to exist in almost every discussion a great deal of confusion surrounding just what it is that makes for a “hard” strike. The purpose of this article is to outline a simplified model of punching that will allow some of the more common conceptual issues to be addressed qualitatively. Also presented is an alternative view of technique which avoids appealing to naïve notions of force as an intrinsic property of moving objects in order to explain the important role played by body mechanics. In no way is the model presented here intended to cover every aspect of punching (nor every misconception!). Rather, it is hoped that the reader will gain from this presentation a greater appreciation of the fundamental physics involved in punching as well as the types of simplifications typically made when approaching real world problems.
In our search for an equation capable of predicting the effect of a technique, we might first come across the definition of momentum. This looks promising at first, as it seems that massive, fast moving objects strike harder than less massive, slower moving ones. On the other hand, I suspect that we should all agree that getting hit by a 1kg object moving at 1000 m/s is a lot less desirable than getting hit by a 1000 kg object moving at 1 m/s, even though they both have the same momentum. It might, therefore, be tempting to single out KE=1/2mv2, instead, as the correct equation to use when trying to determine the outcome of a punch.
The trouble is, this equation doesn’t tell us anything! We have simply given a name to some quantity! We could just as easily have said that the mass needs to be maximized because some other made-up quantity is proportional to the cube of the mass, or is exponential in mass, or whatever. Nothing is actually predicted until we show how one quantity (such as the kinetic energy) is related to some other measureable quantity (or quantities). We should really be seeking a deterministic model of the collision that predicts what will happen when object A strikes object B. And doing so will require a bit more work than hunting through a freshman physics book searching for an equation that has all the “right” variables.
Here is where the modeling comes in. We need to make some reasonable assumptions (and maybe even some not so reasonable ones!) about the physical properties of the colliding objects. Of course they must have some mass (let’s say m and M, respectively) and must collide with a relative velocity v—if they didn’t you might correctly surmise that there would be no collision in the first place! We will also assume, for simplicity, that the target is unsupported.
But what else? Surely hardness makes a difference, and here is where our first approximation must enter: Let’s assume that the force applied by the colliding objects is proportional to how far they’ve been compressed (not an unreasonable assumption provided they are not compressed too far). We could also add other terms that are proportional to the rate at which the objects are compressed, or even the rate at which that rate is changing (whew!), but we’re just looking for a first approximation here, and for the sake of simplicity, let’s neglect all of that for now.
Okay, now we’re going to hit our first real roadblock: Your fist is not some isolated object out in space. There are forces being applied by your muscles, your connective tissues, bones, etc. and we don’t have any idea how important they are. The usual approach is to neglect all of those forces because the collision time is “small”—this means we can pretend that our punching arm and target form a “closed system” and that momentum and energy are (at least roughly) conserved.
Unfortunately, this is not (by itself) very good motivation for saying that momentum is conserved. After all, even if the collision time is on the order of milliseconds, if the external force applied by the puncher’s body is large enough, the system’s momentum can still change appreciably. Here we invoke a model of muscle contraction originally due to Archibald Hill. What Hill discovered is that the force applied by a muscle depends on the rate at which that muscle is contracting (the so-called “contractile velocity”). And it does so in such a way that, as the rate at which the muscle contracts tends toward a “maximum speed,” the force decreases to zero. This will be our motivation for neglecting forces applied by muscle contraction.
Boxers are routinely seen to apply forces on the order of half a ton when striking heavy-bags with a gloved fist. How does the effect of muscle contraction compare to this? It is easy enough to find out: simply assume a punching position and push against a scale held vertically against a wall. You will probably note that the force registered by the scale is significantly smaller (by at least an order of magnitude) than forces typically applied by boxers on heavy-bags. Note also that the actual force your muscles would be applying decreases (per Hill’s relation) with the rate at which they contract. So, even if we were to include our “static maximum” pushing force (which overestimates the actual force we would be applying) in our punching model, the final result will likely not be changed appreciably. We can, therefore, probably safely neglect the force applied by the muscles of the arm (at least during the collision!). [EN1]
We now want to find the maximum force applied during the collision (the force applied when the two objects are moving at the same speed). If we neglect the effect of muscular forces applied during the collision, [EN2] it is then a relatively straightforward bit of algebra to show that (via conservation of momentum and energy)
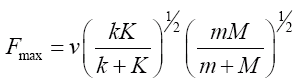 ,
,
where k and K are the “stiffnesses” of the objects with masses m and M, respectively. [EN3]
Interestingly, our intuition about the relative importance of mass and velocity apparently wasn’t too far off for, as M becomes much much greater than m, Fmax becomes v[kK/(K+k)]1/2m1/2. Being struck by a 1 kg object moving at 1000 m/s really is less desirable!
But note that our final result is not simply equal to the kinetic energy, either. Were it so, we should expect a mass of 106 kg moving at 1m/s to do just as much damage as a 1 kg chunk of the same material moving at 103 m/s. Apparently, neither momentum nor kinetic energy is, by itself, a good predictor of the effect of a technique. Indeed, there exists no intrinsic property of a moving object which is sufficient to predict what will happen when a collision with another, unspecified object occurs; collisions don’t happen in isolation!
It is very common to encounter arguments that motion of the more remote parts of the body is important because it increases the mass in F=ma. This conception appears rooted in the naïve notion of force as a property of accelerating objects: Increase the mass of an accelerating object and you increase the “force” that it “has.” Instead, we wish to argue that sequential body movement is of primary importance in increasing limb velocity.
Recall that the change in an object’s kinetic energy is equal to the work done on that object. Now let’s suppose we want to calculate the corresponding velocity. What we would have to do is sum up all of the forces (vectorially) applied to the arm (including those due to muscular contraction) and then multiply that net force by the distance over which it is applied.
Not so fast! Hill’s equation tells us that the muscular part of our net applied force is not a constant but, rather, decreases with the rate at which the muscle contracts! So, if we just multiplied our static maximum muscular force by the total distance over which it is applied, we would overestimate its contribution to v.
But wait! Here’s an idea: We could simply break up the total distance over which the muscular force is applied into very tiny segments—segments soooo tiny that we can consider the force applied over each one to be (essentially) a constant. Then, starting from rest, we would multiply an appropriate initial force by some tiny distance, and then add to that a different (smaller) force (because the muscle is now actually shortening) multiplied by the next tiny distance, and then add to that a (smaller still) force multiplied by the next tiny distance, and then... until the fist has moved all the way to the target.
You might wonder why anyone would want to do this, and, actually, I wonder that myself! However, this analysis is useful in telling us qualitatively what we should do to maximize the velocity of the arm (and, hence, the maximum force applied during the collision):
We want the work done on the arm to be as large as possible so that the impact velocity is as large as possible. But, if we let our torso counter-rotate (or, even worse, deliberately pull back the punching side of the body during the punch) the muscle would shorten at a greater rate, and, according to Hill’s relation, this means that the force applied over one of our tiny distances would be smaller than it would have been had we kept the shoulders fixed in space (or, even better, had we deliberately begun twisting the punching side of the body toward the target prior to throwing the arm forward). Also, because of the limited range of motion of the arm, the total distance over which our variable force is applied in the first case would be less than that in the second case.
But there is even more to it than this: Preceding the extension of the arm relative to the torso by a twisting motion of the shoulders also changes the work done on the arm by taking advantage of the passive elasticity of the muscles, thus increasing the force applied over the first few displacements still further. And finally, because the initial force applied to the arm increases with the length of time the muscle has been “activated” at fixed length, we have yet another reason to precede the motion of the arm with a twisting of the torso.
If we apply the same argument as above to the hips and shoulders, we see that the hips should initially have some angular momentum in order to maximize both the force applied to the punching shoulder and the distance over which that force is applied. And finally, sufficient frictional forces acting at the feet are necessary to ensure that the force applied to the hips (and the distance over which it is applied) is also maximal. To appreciate the importance of this, try hurling a heavy object while standing on ice and compare the results to those obtained while standing on concrete.
A common argument is that, in order to apply a large collisional force, we need as much mass as possible traveling toward the target. In actuality, the mass of the body only matters to the extent that it changes the system’s momentum or energy appreciably; were no force applied by it, it may just as well not have been there.
We have thus far argued that typical muscular torques will likely be much smaller than that due to the collision. However, we do need to take into account the effect of the inertia of the upper arm (at least, for a straight punch) [EN4] and possibly some other parts of the body (though they are often of considerably lesser importance), and this can be done by introducing an “effective” mass that comes from measuring the mass of the struck object along with the speed of both objects before and after the start of the collision. Assuming that the target is initially at rest, we then have
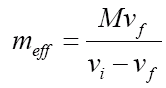 ,
,
where vf is the final speed of the struck object (of mass M) and fist and vi is the initial speed of the fist.
This is generally how researchers have defined effective mass when conducting experiments in boxing and karate, and, interestingly, the measured effective mass falls well short (usually by more than an order of magnitude) of the puncher’s total body mass. The reason for this is more apparent if we take a slightly different (but, I believe, more intuitively appealing) approach by defining the effective mass as
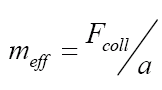 ,
,
where Fcoll is the force applied during the collision and a is the acceleration of the striking surface in the direction of that force.
As is the case with the previous definition, this effective mass is, in fact, dependent on two factors: 1) external forces applied to the striking limb and 2) the orientation of the striking limb during the collision.
The first element is somewhat obvious: If there is an external force applied to the arm during the collision, the arm will accelerate differently (for a given collisional force) than it would have in the absence of such a force.
The effect of the striking limb’s orientation on the effective mass can be understood qualitatively in the following way: For an object that behaves as a rigid body during the collision [EN5] (a better assumption for hook punches than for thrusts, to be sure, but still not bad for a first approach), our expression for the effective mass can be written equivalently as
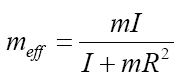 ,
,
where I is the object’s moment of inertia about its center of mass and R is the perpendicular distance between the object’s center of mass and a line extending from and parallel to the collisional force.
Simply speaking, if you were to close your eyes and push on some object, the part of the object in contact with your hand will be easier to accelerate if the push causes the object to rotate somewhat (rather than simply translate). And, if you attempt to move the object without rotation, the effective mass is simply the mass of the object. This should be somewhat obvious as, if you are pushing directly toward the center of mass of an object, you have no way of knowing how the mass of the object is distributed; all of the mass may just as well have been located at the center of mass. We can thus understand the effective mass of an object as the struck area’s apparent resistance to changes in motion.
But note that this effective mass is completely independent of the history of the technique. That is, it matters not whether the hips are still moving during the collision or whether they were used to initiate the motion—when your fist actually collides with the target, the effective mass is entirely determined by the orientation of your body in space. As far as effective mass goes, it doesn’t matter which parts of the body are moving or even whether or not they are moving in the direction of the target! Whatever positive effect the motion of more distant (and, coincidentally, for a punch, more massive) parts of the body has on the outcome of a technique must, then, be limited to increasing the relative velocity with which the striking limb and target collide.
Our earlier reasoning implies that a hammer-fist should have a smaller effective mass than a straight punch (in which the forearm is kept parallel to the collisional force throughout the technique). Does this mean that a straight punch will apply a larger force to the target? Not necessarily. Keep in mind that hammer-fist strikes have generally been shown to have a larger velocity than straight punches. Also, our model predicts that the maximum applied force doesn’t depend simply on the effective mass of the arm but, rather, on the quantity meffMeff/(meff+Meff). This means that, if one is striking an object with a much smaller effective mass than the effective mass of the striking limb, there is little benefit to further increasing the limb’s effective mass. On the other hand, there is always a benefit to increasing the relative velocity with which the objects collide (all else being equal). In short, one cannot say whether this or that technique will “strike harder” without specifying the properties of the object being struck.
Returning to our expression for the effective mass, we see the reason that the entirety of one’s body mass shouldn’t enter into our equation: the effective mass is only equal to the total mass if a force is applied directly toward the center of mass (seldom the case in punching). Keep in mind also that the above relation assumes that the body doesn’t deform at all during the collision. That is, in order to have an effective mass equal to your total body mass, all the agonistic muscles in your body would have to tighten so forcefully that every part of your body undergoes the same acceleration. It should also be noted that high-speed film of tameshiwari shows that the shockwave produced during collision does not actually finish propagating through the entire length of the arm until after the collision. This suggests that our rigid body model somewhat overestimates the actual effective mass of the striking limb even if one is capable of applying muscular forces large enough to ensure that every part of the body undergoes the same (angular) acceleration—at least, in collisions with hard, massive objects.
It might be tempting to see the above discussion as justification for deliberately tightening all of the muscles of the body during the collision—a common admonition in many dojo. This appears to be based on the assumption that, since things which are “hard” don’t deform noticeably under an applied force, the whole body should be made “hard” during the collision (presumably, by tightening everything or “locking down”) so that it doesn’t deform noticeably either. As a simple example, we might consider a vertical pole held stationary by a set of three strings (all under tension) connected to a base on which the pole is mounted. When nothing is pushing on the pole, the torques due to the three strings must exactly cancel one another, and this may seem like justification for “tensing up” during the collision: The pole and base form a cohesive object, and we want our whole body to act like a cohesive object; so, therefore, everything should be tightened, like the strings on the pole. However, in the presence of another force (whether due to a push, a collision, or whatever), the pole and base only act as a single unified object if there is an increased tension in the string(s) applying an oppositely directed torque. And this increase in tension must be larger if there is not a commensurate decrease in the tension of the other string(s). If the tensions in all the strings had remained constant, the pole would have toppled off the base just as easily as if there were no strings at all!
At first glance, this may seem to fly in the face of experience. After all, it is certainly more difficult to bend someone else’s arm at the elbow when that person’s biceps and triceps are activated simultaneously than it is when the arm is completely flaccid. Although it may seem that the muscles on both sides of the arm are under equal tension here, this is certainly not the case. This is because the activated muscles act like elastic structures (very much like the strings in the above illustration) and as the joint begins to bend, the biceps shorten and apply a slightly smaller force at the same time that the triceps are lengthening and being placed under greater tension. The net effect is that as the elbow bends more and more, it becomes more and more difficult to bend it further. This continues until the necessary tension cannot be maintained and the muscle fails. But note that the force required to bend the arm (and, therefore, the effective mass of the arm) would increase if the biceps were to simply remain as relaxed as possible throughout the exercise while only the triceps were activated (the “secret,” if it ever was one, to aikido’s unbendable arm). The idea, then, must be to consciously tighten only the appropriate muscles during the collision rather than all of them indiscriminately.
In more ballistic motions, it is even more important that the tension in antagonistic muscles be minimized. As we saw earlier, the maximum force applied during a collision depends on the speed at which the objects collide, and maintaining tension in antagonistic muscles would act to limit that speed. Some might argue that it could still be advantageous to deliberately employ antagonistic muscle tension if the overall increase in effective mass outweighs the decrease in speed, but we have just seen that antagonistic muscle tension limits the effective mass as well as the speed.
Intentional co-activation of opposing muscle groups is advantageous only in those cases where the agonists and antagonists cannot be unambiguously identified beforehand. As a simple example, one might consider the wrist in a straight punch. Since the primary goal of muscle tension in this area would be to prevent the wrist from collapsing, it might seem that we should simply contract the muscles that oppose the torque due to the collision. But it is not so easy to see which muscles those would be! After all, depending on how the target moves just prior to collision, the impact could cause the wrist to buckle upwards just as easily as it might cause the wrist to buckle downwards or to the side. But because the collision is typically of such short duration, we cannot hope to have enough time to react to this force and then activate the appropriate muscle groups. Instead, we tighten everything in the forearm and fist and allow the elastic properties of the muscles to handle the rest. And we do this knowing full well that it is a second-rate solution to a problem that would have been better solved by simply limiting muscle activation to the agonists, were we able to do so. Sometimes you have to take what you can get.
In developing our simple model, we made passing mention of the “stiffness” of the colliding objects. It may seem that this quantity should be entirely dependent on the material of which these objects are composed, but, if that were really the case, a 1/8 inch diameter steel bar would be no easier to bend than one of 4 inch diameter. Evidently, the intrinsic material property which characterizes how hard a material is to bend is not the bulk “stiffness” but the “stiffness” that characterizes the interactions among the various atoms and molecules of which the material is composed. But since any macroscopic object is made up of many such interacting atoms and molecules, we must apparently know something about their number and arrangement in order to predict the “stiffness” of the object they comprise.
Among other things, this also means that the magnitude of the collisional force will be dependent on the surface area over which that force is applied. To see that this is the case, we might consider the simple example of a vertically held board struck by a reverse punch: As the fist collides with the board, the parts of the board directly in contact with the fist will be compressed a greater amount than the parts further toward the edges of the board. This effectively means that the interaction between board and fist takes place between relatively fewer molecules when the force is applied over a smaller surface area. This decreased interaction amounts to a smaller “effective stiffness” than would have been seen had the collisional force been spread out over a larger surface area and means that the collisional force itself must be diminished.
This is perhaps a slightly counter-intuitive result. Common wisdom holds that, in order to maximize the likelihood that a board is broken, the force should be concentrated over as small an area as possible. So which is it? Actually, both statements are more or less correct: The collisional force really does increase as the area of contact increases, but note that it doesn’t do so exactly linearly—that would only happen if the parts of the struck object not directly in contact with the fist experienced no change in motion whatsoever as a result of the collision. But even those parts of the struck object very far from the collision do experience at least some change in motion as a result of forces applied by the rest of the object. This force, however, is not enough to ensure that adjacent sections of the object experience the same acceleration, and, therefore, there will be some bending of the object about the striking limb. As the target bends, the distance between adjacent molecules on one side of the target increases and, at a certain point, a break occurs. This bending tends to increase as the collisional force is localized to a smaller and smaller area at the center of the object, particularly if the ends are held fixed in space. Because it is not the collisional force, per se, that determines whether a break occurs but, rather, the force applied by adjacent sections of the target on one another, the collisional force really should be applied over as small an area as possible in order to maximize the likelihood of a break occurring.When punching relatively unmoving targets, it will sometimes feel as though one is “rooted” into the ground as a result of the reaction force, and this may seem to underscore the importance of a good stance, having the rear heel on the ground, or “unweighting” the front leg during collision. A common argument is that, without these things, the puncher will be knocked backward, and this must signify some of the “reaction force” having gone “into” the puncher’s body rather than “into” the target. In reality, action-reaction forces are always “equal and opposite” and a larger reaction force applied to one body doesn’t leave less “force” left over to go “into” the other. Surely some will take this to mean that they should always allow their hand to be knocked backward by the collisional force, but this too is wrong since force is not a property of moving objects. In other words, we can’t say that the reaction force was large or small or anything simply by observing whether or not an object was knocked back in the collision.
Basically, the question of whether or not the puncher is knocked backward during the collision is a separate question from whether or not a large force is applied to the target. To answer it, we would have to sum up the forces applied to the puncher. But there is little reason to do this as the net force could easily be large, small, or anything without affecting the force applied to the target.
The feeling of being “rooted” into the ground is largely due to the effect of muscle contraction (i.e. continuing to push the target, in addition to applying a collisional force) and is not a sign that a large force is being applied to the target, either. After all, you should find that you experience the same sensation even when statically pushing against a wall, in which case no collision has even taken place! Although there is no real problem with a little extra push (provided you are not leaving yourself open), the effect of pushing should be dwarfed by the force applied as a result of the collision; if you find that it isn’t, you should probably be moving your fist more quickly! On the other hand, a solid stance and a bit of additional pushing during and after the collision are of some use if you are attempting to stop a massive object from overrunning you. This is because, although the collisional force is typically quite large, it is only applied for a very short time (typically on the order of milliseconds) and is thus often not capable of bringing a violently swinging heavy-bag or rushing opponent to a halt by itself. So, particularly if you are of the sumo wrestling persuasion, go ahead and push all you want: It probably won’t do much damage, but it just might keep you from being trampled—at least momentarily!
A common bit of wisdom is that a heavy-bag should not swing noticeably when struck as this would mean that some of the “force” or “energy” has gone into knocking the bag backward rather than deforming it. But note that the distance the bag swings could well be very large without at all decreasing how much it is deformed. In fact, were we to simply increase the mass of the striking limb while holding all else fixed, the bag would swing to a greater height and experience greater deformation. Indeed, the only case in which a heavy-bag will not swing is if no force is applied to it at all! However, this is not to say that swinging heavy-bags necessarily imply good punches as one could simply apply a small force for a greater length of time (by pushing the bag, for example). In short, punching technique must be evaluated by observing the acceleration or deformation of the bag rather than its swing height alone. But since both of these quantities depend on the mass and hardness of the target, one should take care to train with lighter pads, as well; failing to do so could lead to developing habits which are optimal only for striking more massive objects.
It might at this point be tempting to use our newfound knowledge of physics to re-engineer a few techniques. For example, since we know the dependence of the maximum collisional force on the mass and velocity of the colliding objects, we might be tempted to say that, when executing a straight punch on a very massive object, we should make contact not when the fist is moving at its maximum velocity, as is commonly taught, but somewhat later, when the effective mass is slightly greater. This might sound reasonable at first, until we note that the velocity of the arm decreases very dramatically toward the end of the punch (as a result of connective tissues and muscles applying forces to keep the arm from being wrenched out of its socket). Add to this the fact that the difference between the effective mass of a straight punch at 85% extension is not terribly greater than at 75% extension and we have very little reason to obsess over such minutiae. Sure, the maximum force might be a few percent greater, but, to regularly take advantage of it, we would have to control the distancing at the level of fractions of an inch. In practice, you hit whatever target presents itself with whatever technique seems best suited at the time without regard for whether the opponent is breathing in or out, the position of the big toe, or how much your wristwatch contributes to the effective mass of the technique. We should all recognize that those things partly influence the final outcome (albeit by a small amount), but that need not (and should not) make us slaves to executing particular techniques only when the situation is determined to be ideal to five decimal places.
Neither should our arguments about body mechanics lead us to alter or entirely abandon certain techniques which do not take advantage of sequential body movement, such as boxing-style jabs and lead leg roundhouse kicks in which the motion is limited primarily to the lower leg. Obviously, having an incredibly fast punch isn’t of much use if the opponent is always given plenty of forewarning. It should come as no surprise then that some techniques are not meant to maximize collisional velocity at all—some are just there to distract or set up and some require a compromise between “ideal” body mechanics and situational dynamics for there to be even a remote chance of making contact in the first place. A technique that is capable of maximizing the collisional force but has no hope of landing is worthless for anything other than breaking boards.
Had there not already been so much nonsense written about the physics of karate techniques, the usefulness of our newfound knowledge would be pretty much limited to showing us why knee strikes to the head are more effective if used in conjunction with a grab or that strikes with the back of the fingertips are not effective when executed to the body—the sorts of things that should have been obvious all along. As it is, a bit of sound physics knowledge has some additional use in the dojo as a means of filtering out questionable explanations, but that’s about it. It certainly shouldn’t yield any profound insight into the awesome destructive power of some heretofore unknown technique of our own design—if it seems to, our first step should be to question our reasoning. For a very long time, people have been competing in environments where success is objectively measured, and the associated selection process has resulted in techniques and training methods which are often already well-optimized to achieve a given result. So, whenever we find that what the great majority of successful athletes do is dramatically different from what we believe to be optimal under similar circumstances, it is probably best to ask ourselves why that is. There might be a very good reason. A little knowledge can be a dangerous thing.
If there is one point to take away from any of this it is that the force applied during a collision depends just as much on the properties of the object being struck as it does on the one doing the striking. We are thus directly confronted with the fact that force is not an intrinsic property of the punch (or puncher). Rather, it is a way of characterizing an interaction between two objects. Phrases such as “the force of a punch” are, therefore, nonsensical as no force is applied until there is an interaction, and the magnitude of the applied force will depend markedly on the characteristics of that interaction.
Neither are we justified in arguing that proper form is instrumental in “channeling” reaction “forces” harmlessly into the ground or “focusing” them back into the target. The argument that reaction “forces” must be minimized or “harnessed” in some way during a collision appears to be rooted in the dubious notion that objects have only so much “force” in them, and greater “force” going “into” the puncher means less “force” going “into” the target. On the contrary, force is not a conserved substance, and (per Newton’s third law) a larger force applied to the striking limb automatically implies a larger force applied to the target. The common (naïve) picture of force as either a transferable substance or a property of moving (or accelerating) objects must be among the first bits of intuition discarded if one is to develop any meaningful understanding of collisions (or physics, in general).
There is also a rather wide-spread notion that F=ma implies that, in order for the collisional force to be large, the duration of contact must be as small as possible and this justifies pulling the fist back as it makes contact with the target. It should be noted, however, that in our collision model the duration of the collision is determined entirely by the properties of the colliding objects. Pulling the fist back as it contacts the target simply decreases the maximum compression of the struck object (and, hence, the maximum collisional force). Even if the fist happens to undergo a greater change in momentum per unit time in a “snapping” punch, it must be realized that this is due to a force (applied by the puncher) pulling the fist away from the target and not a larger force being applied to the target itself.
Readers favoring an energy based approach to collisions should take note of the connection between our simple model and ones based on a coefficient of restitution: When the collisional force is a maximum, the objects are moving at the same velocity. Thus, were we to specify that the collision ceases at that point (due to the breaking of one or both objects), we would be left with a coefficient of restitution equal to zero, and the kinetic energy lost during the collision would be equal to that required for the break(s) to occur. If, on the other hand, no break occurs, the change in the total kinetic energy of the system would now equal the energy associated with the resulting vibrations of the colliding objects. This should not, however, be taken as evidence that our simple model predicts coefficients of restitution. The coefficient of restitution for a given collision depends, in general, on a great many factors and is, in real materials, itself a function of the relative velocity of the colliding objects. This complex behavior requires empirical testing but can lead to a much more reliable picture of some aspects of collision dynamics (such as the generally greater significance of velocity than our simple model predicts) provided the coefficient of restitution for a given collision is well studied. I have chosen not to take such an approach in this essay as, in my experience, many fundamental misunderstandings of the nature of force are too easily concealed by the wholesale application of energy considerations. Because kinetic energy, unlike force, is a property of moving objects, at least some of our naïve intuition (which is obviously inadequate for the understanding of forces) can often seem relatively palatable from an energy standpoint. This makes it far easier to unknowingly lapse into intuitive conceptions of physics and arrive at conclusions as questionable as those based entirely on naïve reasoning.
There is much here that is left unexplored. Notably, the influences of nonzero external force, viscous drag, and local deformation of the colliding objects on the maximum collisional force are not accounted for by our simple model. While the addition of these effects introduces many interesting avenues of study, the purpose of this essay has not been to entirely exhaust the topic of collision dynamics (indeed, there exists a small sub-field of engineering devoted to this subject). Instead, we have merely introduced a simplified model capable of accounting for some of the most readily apparent behavior observed in collisions with the aim of illuminating some common misunderstandings of fundamental physics and its application to karate. Some readers may object that our approach has been too simple—that, in neglecting some of these complexities, we have ignored the phenomena that make a karate technique fundamentally different from those seen in boxing or muay thai. Admittedly, there is a remote possibility that this might turn out to actually be the case. Until now, however, claims of the uniqueness of karate technique have been largely based on fundamental misunderstandings of the underlying physics, and, as long as these persist, adding complexity to the problem is unwarranted and unlikely to result in significant insight.
Over
the past sixty years or so of karate’s history, a great deal of
misinformation and questionable physics has flooded books and dojo
alike—the typical arguments serving less as science than as
justification for stylistic dogma. While there does exist a great
deal of very good (even excellent) coaching advice in karate circles,
it is unfortunate that many instructors feel qualified to offer
explanations of phenomena outside their realm of expertise. In
particular, because instructors are often unfamiliar with the
reasoning required to develop deterministic collision models, they
are forced, instead, to resort to ad
hoc
explanations and misapplied equations in elaborate attempts to
justify what would perhaps otherwise be entirely useful instruction. In
the best case, this is merely a harmless waste of training time. In the
worst case, it can result in the development of highly
questionable techniques and training practices which serve as a
hindrance to the progress of earnest students. It is hoped that the
above (very) simple model will remedy the dearth of material in
karate circles concerning the modeling of collisions and serve as a
springboard toward the reader’s further understanding of the
dynamics of impact.
EN1 For simplicity, we will consider the case in which the torso undergoes no appreciable change in its angular or linear velocity during the collision (this is equivalent to assuming that the torso’s mass and moment of inertia are infinite). The sum of the torques (about the shoulder) applied to the upper arm is
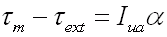 ,
,
where τm is the torque applied by the relevant muscles, τext is the torque applied by the forearm on the upper arm, Iua is the moment of inertia of the upper arm about the shoulder, and α is its angular acceleration.
Similarly, for the forearm/fist,
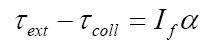 ,
,
where τext is the torque applied by the upper arm on the forearm, τcoll is the torque applied by the collision, and If is the moment of inertia of the forearm and fist about the shoulder.
If the elbow joint does not deform too greatly during the collision, the angular acceleration experienced by the forearm must be the same as that experienced by the elbow. Then
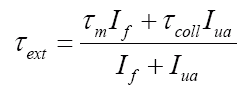 .
.
We would be unjustified in neglecting the torque applied by the muscles if it is on order of the torque applied by the forearm to the upper arm:
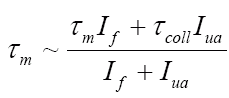 .
.
A small bit of algebra shows that this is only the case when the torque applied by the muscle is comparable to that applied by the collision (provided the moment of inertia of the forearm and fist is not orders of magnitude larger than the moment of inertia of the upper arm—in which case we wouldn’t need to worry about anything except the forearm and fist). But applying equilibrium conditions to our simple scale experiment shows that, at most, τm~τscale. Therefore, as long as Fcol l >>Fscale, we can safely neglect the torque applied by the muscles.
[EN2]The astute reader may protest at this point, saying that we must still contend with an external force applied by the parts of the body in contact with the arm. This is absolutely true. However, it turns out that not all external forces are created equal; external forces which are themselves determined by the collisional force introduce no difficulty at all, provided we define “mass” appropriately, and this will be done later. The question of the applicability of our simplification is then reduced to the question of whether or not external forces which are independent of the collisional force can be safely ignored.
[EN3]It bears mentioning at this point that the above relation assumes that the two colliding objects can be modeled as completely rigid masses with massless spring “bumpers” attached to one side. Because any macroscopic object is really made up of a collection of particles (each of which has some mass), it is not immediately apparent that our model has much to do with the behavior of real colliding objects. It turns out, however, that, when a force is applied to some object in equilibrium, the molecules nearest to the point of application of the force are squished together much more than the molecules making up the rest of the object. This means that the deformation of the object is localized to a region of much smaller mass than that of the object as a whole. Therefore, at least in equilibrium, a macroscopic object can often be well modeled as a combination of perfectly rigid point particle and massless spring “bumper.” The question is then whether or not this behavior also applies to collisions (in which case neither object is in equilibrium).During the collision, the molecules that comprise the colliding objects do, indeed, undergo very complicated changes in motion, but, in a very short time, their relative motions start to cancel one another out—the complicated oscillations decreasing in amplitude and becoming more random. As this occurs, the object as a whole begins to deform just like an object in an equilibrium situation (even though it is, of course, still accelerating). The length of time required for all of this to take place is on the order of the length of time it takes for a sound wave to traverse the length of the colliding objects a dozen or so times. Our model’s applicability is then limited to those collisions in which this time is shorter than the duration of the collision and deformation is localized to the area directly in contact with the target. High-speed footage of tameshiwari, however, shows that the fist and forearm experience some relative motion during the collision, and, thus, the two do not behave like a completely rigid object. A much better model would, therefore, have to separate the striking limb into segments of different mass and then include a massless spring between those segments. Unfortunately, it is not so easy to see that such a model would be analytically solvable. In any case, we are just interested here in obtaining some rough qualitative idea of what happens when objects collide with one another. Were we to worry ourselves about the exact detailed behavior of each and every molecule that makes up the colliding bodies, we would find very quickly that we have made the problem completely intractable, and this would prevent us from beginning to understand even the most basic aspects of collision mechanics. That making some headway in our understanding of collisions does not require a detailed knowledge of (or even a passing familiarity with) all these complexities is quite a remarkable fact—and a necessary one at that! Indeed, the entire enterprise of science would be doomed at the outset were this not the case.
[EN4]To see why this is the case, we simply sum up the torques (about the shoulder) applied to the forearm (again assuming, for simplicity, that the torso undergoes a negligible change in translational and rotational velocity):
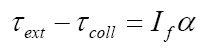 ,
,
where τext is the torque applied to the forearm by the upper-arm and If is the moment of inertia of the forearm.
And, similarly, for the upper arm (neglecting the comparatively small torque applied by the muscles):
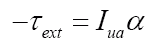 .
.
Then, assuming, again, that the arm does not deform too greatly,
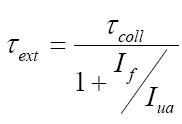 .
.
We see then that τext << τcoll only when If >> Iua; should we not include the (effective) mass of the upper arm in a straight punch, we would have to consider the effect of an external force (applied by the upper arm).
[EN5] So what do we do if the body doesn’t behave as a completely rigid body during the collision? As a simple example, we might consider two sticks connected by a swivel joint. If a force is applied to one of the sticks, it will begin to accelerate. But, because of the joint, the other stick will itself begin to accelerate as a result of the force applied to it by the first stick. If we add the constraint that the acceleration of the ends of the two sticks connected to the joint must be the same, we can derive a relation for the effective mass of this simple two-stick system. The extension of this model to the human body is then (conceptually, at least) relatively straightforward: we simply find an equation of motion for each relevant bone in the body and then demand that the acceleration of adjacent ends of each set of two different bones be the same. Although it is more complicated, this approach is capable of taking into account the effect of each and every part of the body on the effective mass. And, if we simply include the earth in our set of interacting objects, we need not even concern ourselves with complicated effects due to frictional forces applied at the feet (provided the feet do not slip during the collision).
Revisiting the simple two-stick example, we see that we could have more easily arrived at the same answer by first finding the effective mass of the stick farthest from the push. We then simply add this effective mass to the joint end of the stick being pushed (as though it were a point mass). The effective mass of this hypothetical stick with a point mass on the end is the same as the effective mass of the real two-stick system. This recursive approach would make the extension of a “jointed rigid body” model to human motion much more trivial.
There is, however, another issue with our model which now arises: If the relative orientations of the various parts of the striking limb vary wildly during the collision, our earlier result for the maximum force is no longer justified. This is because we assumed, in its derivation, that the (effective) mass of the colliding objects was held fixed. But if the striking limb bends or straightens dramatically over the course of the collision, it will behave as though it has a different mass at different stages of the collision. As long as the collision is of sufficiently short duration, we need not concern ourselves with this issue. It is mentioned here merely in the interest of completeness and not because it is likely to introduce any dramatically different behavior—in developing any model, it is always a good idea to see how far it must be taken before breaking down. In our case, this model doesn’t do well with low-velocity collisions against very soft, but relatively massive targets. But, of course, we already knew that since, in such collisions, the external forces applied by muscle contraction (i.e. pushing forward and overrunning the target, sumo-style, after punching) can no longer be neglected.